I did the Ludum Dare, and it was very fun and neat. But the game I made turned out to be quite confusing; even I have been trying to figure out the best way to get a high score. So in this post I’ll do my best to explain what the mechanics are and how everything works (in theory at least), and if you have any questions, feel free to ask.

If you aren’t sure what’s going on, the idea is that you’re at the end of the universe, when all stars, galaxies, and worlds have long since disappeared, and all that’s left is the dead cores of those stars; black dwarfs, neutron stars, and black holes. Not only are they drifting apart at an exponentially faster rate due to the expansion of the universe, but they’re losing mass and will eventually disappear forever.

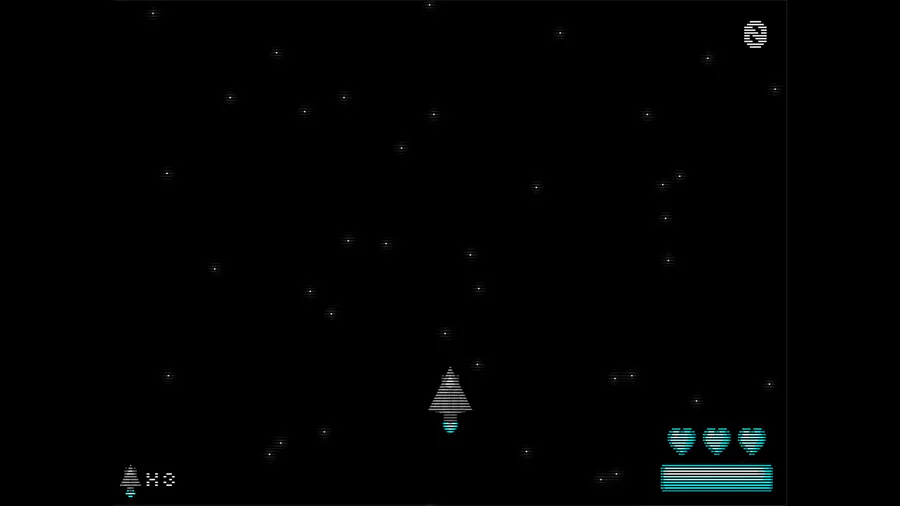
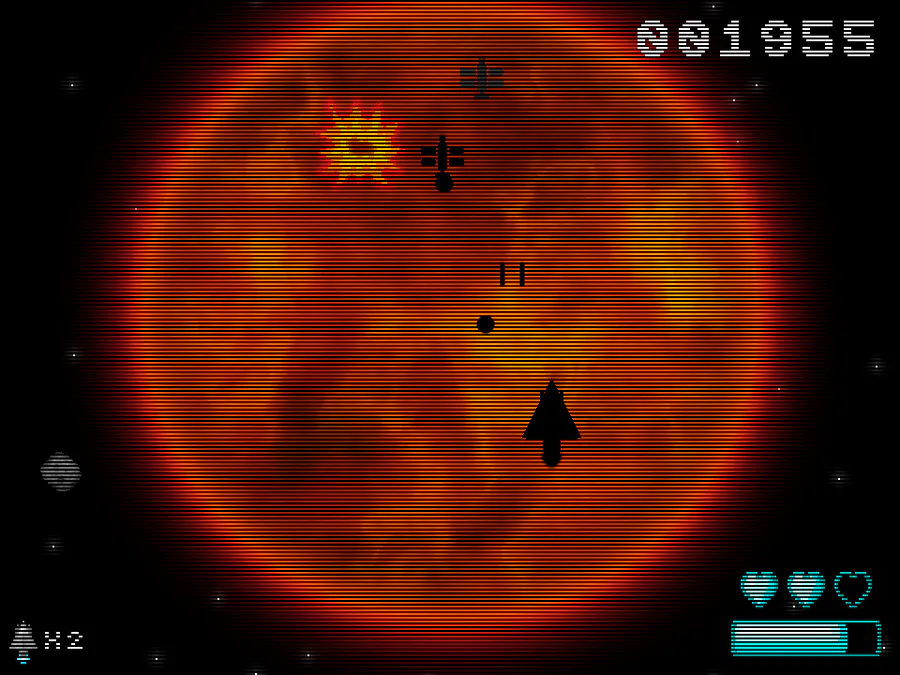
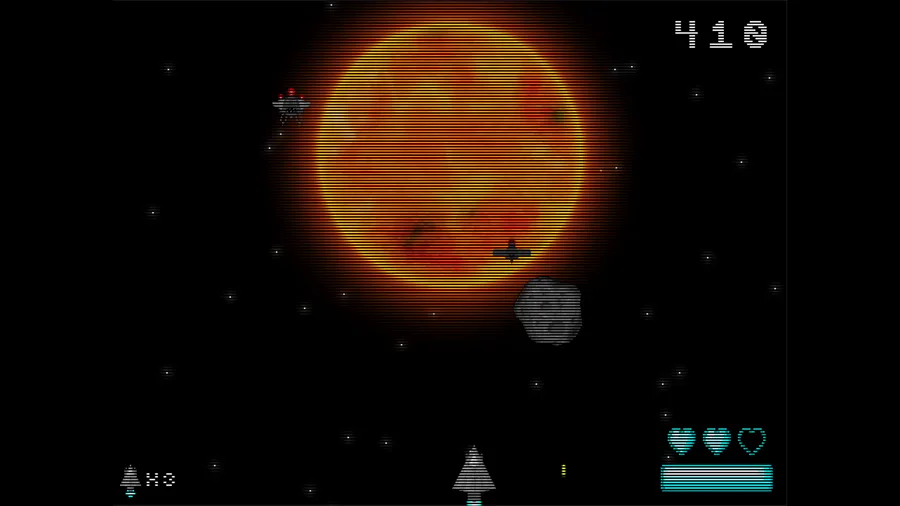
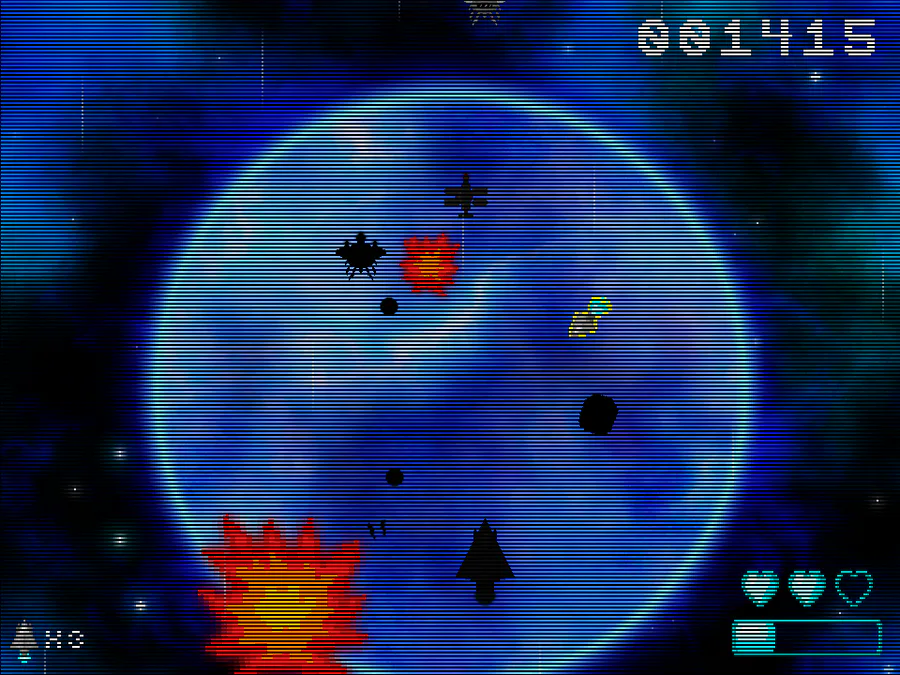
To survive and keep your ship running, you need to acquire energy from stars you find. Your score is the energy you have by the time all objects in the universe either die or are too far away to reach, which is when time reaches 500, and if you run out of energy before then, your score is 0 and it’s game over.

The first thing you’ll need to know is that every stat in the game is one to one.

• 1 unit of mass is equal to 1 unit of energy. When you siphon a star, you gain energy equal to its mass.

• Distance and time are the same, because the distance between stars is measured in the time it takes to reach them. So the first 2 stats the game displays measure the same thing; the time/distance since the game started, and since the last star you visited.

• A star’s mass is also equal to its remaining lifetime. Over time you’ll find less and less stars, not just because of the expanding universe, but also because any stars with less mass than the time that passed disappears.

For every 1 unit of time you spend traveling, you lose 3 energy, so you’re challenged with deciding to siphon a star’s mass or farm its radiation for a portion of the star’s lifespan. You won’t lose energy while farming, and the amount of energy you’ll gain increases with the star’s mass and the time you spend farming, but you’ll also diminish your chances of finding more stars the longer you farm. So the strategy isn’t in choosing whether to siphon or farm, but in how long to farm before you siphon.

Some other things to keep in mind:

• Black dwarfs don’t radiate, so their mass is siphoned automatically. The game displays how many black dwarfs you found and how much energy you got from them. Also, the distance since the last visited star doesn't include them; instead it's since the last neutron star or black hole.

• It’s possible to farm a star past time 500, but you won’t find another star after that, and the game will end.

• A lot of things are randomized, so your success is pretty heavily based on chance. You might find yourself making decisions in hopes of getting lucky.

Here’s some exact math and values:

• 100 is 1 solar mass (the mass of the sun), neutron stars can have a mass between 150 and 250, and stars with more mass are black holes.

• To determine the mass of a star, the game chooses a random number between 1 and 500, and then subtracts another random number between 1 and 500, and takes the absolute value of the result (in case it’s negative). This makes more massive stars less common.

• Before generating a star’s mass, time increases by a random number between ⅛ of the current time and ¼ of the current time. This repeats until a star with mass larger than the current time is generated.

• When you farm radiation, the energy you gain per unit of time is equal to 1% of the star’s mass at that time for every 100 mass it has (if it has less than 100 mass, it still gives 1%). If you farm a star with 300 mass for half of its lifespan, you’ll get 3% of its mass in energy at first, but by the time you’re done farming, its mass will be 150 and you’ll only be getting 1% of that.

Now here’s the thing. This is all how the game is supposed to work. It probably doesn’t. I am not a scientist, I just think this stuff is really cool. In reality, these numbers are way larger and the equations are far more complicated, and I chose balanced game mechanics over factual accuracy.

But also, I probably made some mistakes even with my own math and code. This is my first purely strategic game, I had 3 days to make it, and I’m also just not that good at math. I was figuring out how to play this game as I was making it. But I do think I came up with something interesting, at least.

If you have any questions, feel like I missed something, or found a problem somewhere in my logic or in the game, please feel free to ask about it. I’d be happy to explain something, or point you towards a more reliable source, and if my math is wrong I’ll do my best to fix it.