Wanna know how to make a tower defence game more balanced and fun? I applied mathematics to one of my old games to tighten the difficulty and reduce the power gap between towers. I will describe how I did that at the end of the devlog.

Exactly 18 months ago today I created a basic tower defense game.

Now that I actually know how to make a game I wanted to complete this project. I released the original version, 0.1.0 (which is surprisingly not broken) a few days ago. Since then I reprogrammed several sections of code, cosolidated code into functions, fixed confusing and contradicting statements and conditionals, and fixed some bugs. It still doesn’t look great under the hood but I can deal with that.

Here are the 0.2.0 changes:
-Enemy movement speed is halved
-Towers can target the first enemy, strongest enemy, nearest, and more
-Towers now have names and descriptions
-All towers now shoot roughly 1/3 the speed
-The purple tower now acts like a shotgun
-The blue tower is now a combination of the octo-shot (the basketball-looking one) and the shotgun
-The blue lighning tower shoots slower than before, but the orange lightning tower shoots faster. Earlier the orange and blue towers shot the same speed, but orange had longer range; now they have the same range, but orange has faster speed.
-A few graphical adjustments

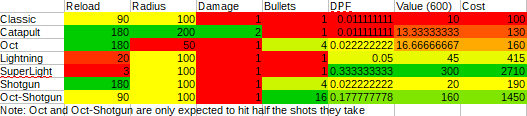
Here’s how I balanced the towers. First, I determined a way to find out the objective value of each tower on a given stage: how many enemy health points can it destroy on its own each wave? I created this formula: value=dpf(srte+tc/es). In other words, damage equals damage divided by frames times frames.
-dpf is damage per frame, which is number of bullets expected to hit the enemy times the damage those bullets deal, divided by the reload speed.
-sr is the enemy spawn rate, the number of frames between enemies spawning
-te is total enemies that will spawn
-tc is track coverage, which is roughly the diameter, twice the diameter on a good day. I’ll call it 1.5 times diameter
-es is enemy speed

The only time the radius changes the proportional values of the towers is when srte is involved, so for the sake of calculating a constant value I will arbitrariy choose that sr=15 and te=40. This makes most of the values whole numbers. Instead of calculating the price of each tower directly proportional to the value, I will make more valuable towers relatively cheaper. Instead of price=nval, I have price=n*val+c, a line with a y-intercept greater than 0. With carefully-chosen values of n and c, I can determine the prices: