Comments
Orbiter
This is simple "space game" featuring a mini-rocket orbital vehicle situated nearby a very small planetary body. The goal is simple enough--see if you can get the vehicle into a stable orbit. Of course, this may be easier said than done; but it is possible using such tools as the laws of Kepler and Newton...
Controls
Keyboard up arrow: Forward (main) thruster
Keyboard down arrow: reverse ("brake") thruster
Keyboard "z" key: z- (left) thruster
Keyboard "x" key: z+ (right) thruster
Keyboard "y" key: y- (down) thruster
Keyboard "u" key: y+ (up) thruster
Keyboard "w" key: pitch up thruster
Keyboard "s" key: pitch down thruster
Keyboard "a" key: yaw left thruster
Keyboard "d" key: yaw right thruster
Keyboard "q" key: roll left thruster
Keyboard "e" key: roll right thruster
F1: take Camera 1 (stationary camera)
F2: take Camera 2 (ship rear, "pilot" camera)
F3: take Camera 3 (ship front, "observation" camera)
Pan/tilt for all cameras: mouse right click and drag
Keyboard "r" key: reset the simulation
Notes:
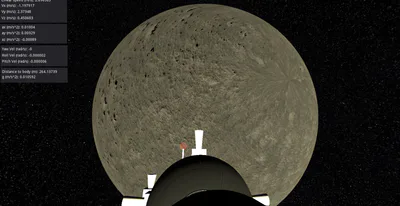
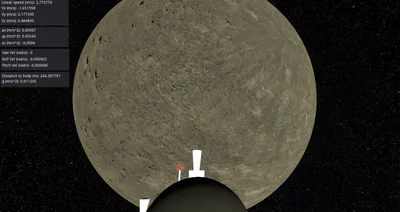
The "instrument" panels will give the following information:
Magnitude of the ship's total velocity vector ("Linear Speed")
Linear velocity vectors in x, y, and z directions in the ship's coordinate system. These are labeled "Vx," "Vy," and "Vz," respectively.
Linear acceleration vectors in x, y, and z directions in the ship's coordinate system. These are labeled "ax," "ay," and "az," respectively.
Angular velocity vectors in the ship's coordinate system for yaw, roll, and pitch
Distance of the ship from the surface of the planet ("Distance from Body")
The value of "g" based upon the ship's distance from the planet
A couple of details on the ship and the planet:
The mass of the ship is set to 1 kg
The radius of the planet is 400 meters
The mass of the planet is 7*10^13 kg. This gives the average density ~ 261,113 kg/m^3. Of course, this is not physically realistic, but to keep the simulation manageable, we use this value. In turn, this gives a value for "g" at the surface of ~0.03 m/s^2.
To keep things simple, the planet has no atmosphere. It is stationary and does not rotate.
Simulation created by Bernard Hall